Matematika Bangun Datar - Lingkaran

Lingkaran

Untuk lingkaran, saat ini masih bagian perhitungan dasar.. Untuk perhitungan lanjutan insya allah akan dibahas di blog mendatang..

Pengertian Lingkaran

Kalau dari wikipedia, lingkaran adalah himpunan semua titik pada bidang dalam jarak tertentu, yang disebut jari-jari, dari suatu titik tertentu, yang disebut pusat.

Kalau dari referensi lain, lingkaran adalah kumpulan titik-titik yang membentuk lengkungan tertutup, di mana titik-titik pada lengkungan tersebut berjarak sama terhadap suatu titik tertentu. Titik tertentu itu disebut sebagai titik pusat lingkaran.

Rumus-rumus dasar lingkaran
Keliling lingkaran
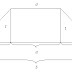
Keliling lingkaran adalah panjang garis luar lingkaran dari satu titik hingga menuju titik itu lagi. Jika kita umpamakan garis luar itu adalah tali, maka garis itu dapat kita potong dan kita hitung panjangnya.
Coba kita lihat lingkaran di samping ini:
Kita potong pada titik X, lalu kita buat menjadi garis lurus.

Jika diukur.. antara garis tengah (diameter) lingkaran dengan panjang garis yang kita tarik tadi itu mempunyai perbandingan yang konstan (tetap).

Dari sinilah konstanta (ketetapan) tentang π (phi) didapatkan.
Jadi pengertian phi adalah, sebuah konstanta dalam matematika yang merupakan perbandingan keliling lingkaran dengan diameternya.

Jika dirumuskan akan menjadi:

Keliling lingkaran = π x d (phi dikali diameter lingkaran)

Luas Lingkaran

Luas lingkaran adalah luas daerah yang dibentuk oleh lingkaran itu sendiri.

Seperti yang diketahui, luas lingkaran adalah : π x r x r (phi dikali jari-jari dikali jari-jari). Atau juga bisa disingkat dengan πr².

Trapesium

Pengertian Trapesium

Trapesium adalah suatu bangun dua dimensi segi empat yang mempunyai dua sisi yang sejajar namun panjangnya tidak sama.

Trapesium yang sisi ketiganya memiliki sudut 90 derajat terhadap sisi yang sejajar disebut trapesium siku-siku.

Rumus-rumus Trapesium

Keliling Trapesium

Keliling trapesium adalah jumlah dari sisi-sisi trapesium itu sendiri. Dikarenakan sisi-sisinya yang tidak sama maka hanya dapat dirumuskan sebagai berikut:

Keliling Trapesium	=	Jumlah seluruh sisi trapesium
	=	a + b + c + d

Luas Trapesium

Luas trapesium adalah 1/2 x (jumlah sisi sejajar) x t.

Mengapa demikian?

Disini akan dijabarkan mengapa demikian.

Trapesium adalah bangun yang terbuat dari dua jenis bangun datar lainnya, yaitu persegi panjang dan segitiga.

Jika kita kupas kembali, luas dari persegi panjang adalah p x t dan luas segitiga adalah 1/2 x alas x t

Karena itu dapat dibuat persamaan sebagai berikut :

Luas Trapesium	=	L segitiga 1 + L persegi panjang + L segitiga 2
Luas Trapesium	=	(1/2 x alas1 x tinggi) + (panjang x lebar) + (1/2 x alas2 x tinggi)

Jika kita masukkan variabel yang ada pada gambar, maka akan menjadi seperti ini:

Luas Trapesium

=

(1/2 x t) + (a t) + (1/2 y t)

Lalu kita gunakan sifat distributif:

Luas Trapesium

=

(1/2 x + a + 1/2 y) (t)

Lalu kita gunakan lagi distributif untuk penguraian (1/2 x + a + 1/2 y) dengan cara dibagi 1/2:

Luas Trapesium	=	1/2 (x + 2a + y) (t)

karena 2a = a + a, maka dapat berlaku seperti ini:

Luas Trapesium	=	1/2 (x + a + a + y) (t)

lalu menggunakan metode subsitusi pada (x + a + a + y) menjadi:

Luas Trapesium	=	1/2 (a + (x + a + y)) (t)

dikarenakan (x + a + y) = b, maka dapat kita ganti menjadi:

Luas Trapesium	=	1/2 (a + b) (t)

Begitulah, kita dapatkan rumus 1/2 x jumlah rusuk sejajar x tinggi

Layang-layang

Pengertian layang-layang

Layang-layang adalah salah satu bentuk dari bangun datar. Dimana layang-layang itu adalah bangun dua dimensi segi empat yang mempunyai dua pasang rusuk yang sama panjang, dan memiliki dua buah pasang sudut yang bukan siku-siku yang mana sudut yang sama besar saling berhadapan.

Definisi lain dari layang-layang adalah bangun dua dimensi yang dibentuk oleh dua segitiga sama kaki yang mempunyai panjang alas yang sama dan memiliki tinggi yang berbeda.

Rumus Layang-layang

Keliling Layang-layang

Keliling layang-layangadalah jumlah dari keempat rusuk layang-layang itu sendiri. Karena memiliki dua pasang rusuk yang sama, maka dapat disimpulkan bahwa keliling layang-layang adalah dua kali dari rusuk pendek ditambah dua kali dari rusuk panjang.

Dapat dirumuskan:

Keliling layang-layang = rusuk pendek + rusuk pendek + rusuk panjang + rusuk panjang
= 2 x rusuk pendek + 2 x rusuk panjang
= 2 x (rusuk pendek + rusuk panjang)

Luas Layang-layang

Seperti halnya belah ketupat, luas dari adalah hasil kali dari 1/2 x diagonal 1 x diagonal 2. Mengapa demikian? Karena apabila dijumlahkan luasnya akan sama dengan luas dua buah segitiga sama kaki yang mana luas dari segitiga sama kaki adalah 1/2 x alas x tinggi

Menurut dari gambar, dapat disimpulkan bahwa diagonal 1 = tinggi segitiga sama kaki 1 + tinggi segitiga sama kaki 2 dan diagonal 2 = alas.

Jika kita masukkan ke dalam persamaan:

Luas layang-layang	=	L segitiga sama kaki 1 + L segitiga sama kaki 2
	=	(1/2 x alas x tinggi 1)+(1/2 x alas x tinggi 2)
	=	1/2 x alas x (tinggi 1+ tinggi 2)
	=	1/2 x d2 x d1 //d2 = alas dan d1 = tinggi 1 + tinggi 2
	=	1/2 x d1 x d2

Matematika Bangun Datar - Belah ketupat

Hmm.... Mari kita makan ketupat..

Eh.. Bukan.. Mari kita bahas tentang belah ketupat..

Pengertian Belah Ketupat

Belah ketupat adalah salah satu bentuk dari bangun datar. Dimana belah ketupat itu adalah bangun dua dimensi segi empat yang mempunyai empat buah rusuk yang sama panjang, dan memiliki dua buah pasang sudut yang bukan siku-siku yang mana sudut yang sama besar saling berhadapan.

Definisi lain adalah belah ketupat adalah bangun dua dimensi yang dibentuk oleh dua segitiga sama kaki yang sama.

Rumus-rumus dalam belah ketupat

Keliling belah ketupat

Keliling belah ketupat adalah jumlah dari keempat rusuk belah ketupat itu sendiri. Karena memiliki panjang rusuk yang sama, maka dapat disimpulkan bahwa keliling belah ketupat adalah empat kali dari rusuk belah ketupat.
Dengan kata lain:

Keliling = s + s + s + s
= 4 x s

Luas belah ketupat

Luas dari belah ketupat adalah hasil kali dari 1/2 x diagonal 1 x diagonal 2. Mengapa demikian? Karena apabila dijumlahkan luasnya akan sama dengan luas dua buah segitiga sama kaki yang mana luas dari segitiga sama kaki adalah 1/2 x alas x tinggi.

Menurut dari gambar, dapat disimpulkan bahwa tinggi segitiga = 1/2 dari diagonal 2 dan alas = diagonal 1.

Jika kita masukkan ke dalam persamaan:

Luas belah ketupat	=	L segitiga sama kaki + L segitiga sama kaki
	=	L segitiga sama kaki + L segitiga sama kaki
	=	2 x L segitiga sama kaki
	=	2 x (1/2 x alas x tinggi)
	=	2 x (1/2 x d1 x (1/2 x d2))
	=	d1 x (1/2 x d2)
	=	d1 x 1/2 x d2
	=	1/2 x d1 x d2